LE ARMONIE DEI PIANETI. Rapporto tra musica e scienza sulle orme di Keplero.

di Simonetta Ercoli

«[Essi] non sono altro che un perenne concento (razionale e non vocale), attraverso intonazioni dissonanti, come certe sincopi o cadenze (e qui gli uomini imitano queste dissonanze naturali), che tende verso clausole fisse e prescritte, particolari dei sei termini (come fossero voci), e segna e distingue attraverso queste note l’immensità del tempo; e da qui non è più una sorpresa che l’uomo, scimmia del suo creatore, abbia finalmente scoperto un modo di cantare in armonia [per concentum], ignoto agli antichi, in modo che egli possa esprimere, per mezzo dell’accordo artistico di molte voci, l’immensità di tutto il tempo del mondo nel breve spazio di un’ora, e che possa in qualche modo assaggiare la soddisfazione del Dio Creatore per la sua opera, in questo soavissimo senso di piacere suscitato da questa imitatrice di Dio, la musica» Keplero, Harmonices mundi, p. 328.

Presentazione generale

“StarLight, un planetario… tra le dita” ha sviluppato un percorso volto alla scoperta delle consonanze esistenti nell’universo secondo il pensiero kepleriano. L’idea di “armonia del mondo” ha permeato tutto il lavoro scientifico di Keplero: i suoi libri Mysterium cosmographicum, Astronomia Nova e Harmonices mundi evidenziano il complesso lavoro che egli ha condotto nell’arco di venti anni, seguendo il nuovo metodo scientifico introdotto da Galileo Galilei. Attraverso calcoli, ricerche, scoperte, modifiche e aggiustamenti voleva mettere in luce i modelli geometrici originari, che Dio impiegò nella creazione del mondo e nell’organizzazione dei pianeti. Il pensiero dominante dell’epoca non prescindeva mai dall’esistenza di un Dio creatore all’origine della perfezione del tutto: un ordine e un’armonia perfetti e valutabili attraverso la matematica e soprattutto la geometria. Ed è attraverso queste scienze che Keplero cercò di portare alla luce i rapporti numerici esistenti alla base del sistema organizzato, che tiene uniti i pianeti e il Sole. Come le distanze dei pianeti dal Sole rappresentano rapporti precisi così le consonanze musicali esprimono un rapporto preciso: partendo da questa convinzione Keplero intraprese la ricerca sulla corrispondenza tra gli uni e gli altri.

Introduzione

Le onde sonore

Un fenomeno sonoro o suono, cioè ciò che udiamo, è il risultato della propagazione di energia e non di materia: un’onda elastica. Ogni volta che in una sorgente si crea una perturbazione, l’energia prodotta si propaga sinusoidalmente nel tempo e nello spazio sotto forma di onde. Se le grandezze fisiche coinvolte sono campi elettrici e magnetici, le onde sono elettromagnetiche; se la grandezza fisica coinvolta è la pressione nel mezzo, si manifestano le onde elastiche, quali ad esempio le onde sonore.  Queste ultime, avendo bisogno di un mezzo in cui propagarsi, a differenza delle onde elettromagnetiche, non si propagano nel vuoto. In conseguenza di ciò la velocità di propagazione del suono è notevolmente più bassa (circa un milione di volte) di quella della luce.

Ogni fenomeno sonoro si sviluppa in quattro fasi:

1. produzione di onde meccaniche ad opera di una sorgente (sorgente sonora) che vibra in conseguenza di uno “spostamento d’aria” (ad esempio le nostre corde vocali, una corda percossa, una membrana, una colonna d’aria);
2. propagazione delle onde attraverso un mezzo elastico (di solito l’aria) in modo ondulatorio;
3. ricezione e percezione dell’onda sonora da parte di un opportuno apparato in grado di trasformare l’energia sonora in altra forma di energia (ad esempio l’apparato uditivo umano);
4. elaborazione del segnale trasformato (in genere in impulsi elettrochimici) da parte del cervello.

Ed è regolato da:

• Parametri oggettivi, cioè le grandezze fisiche che descrivono le vibrazioni delle sorgenti sonore e che caratterizzano l’onda sonora e la sua propagazione, quali la frequenza, la lunghezza d’onda, la velocità di propagazione, ecc.
• Parametri soggettivi, dipendenti dall’elaborazione a livello sensoriale e cerebrale dello “stimolo” sonoro da parte del soggetto che lo riceve, quali l’altezza, l’intensità, la gradevolezza, la consonanza, l’armonia.

La perturbazione dell’onda sonora induce nel mezzo circostante (di solito l’aria) una variazione di pressione in grado di propagarsi come una successione di rarefazioni e condensazioni, cioè di variazioni di densità dell’aria, dovuta all’oscillazione subita dalle particelle attorno ad una posizione di equilibrio senza essere trasportate lontano; l’oscillazione locale delle molecole avviene nella stessa direzione di propagazione dell’onda, per questo viene detta onda longitudinale. L’analisi quantitativa del fenomeno porta alla definizione delle proprietà dell’onda:

• il periodo T della perturbazione è il tempo che la molecola di riferimento impiega a compiere un’oscillazione completa attorno alla sua posizione di equilibrio.

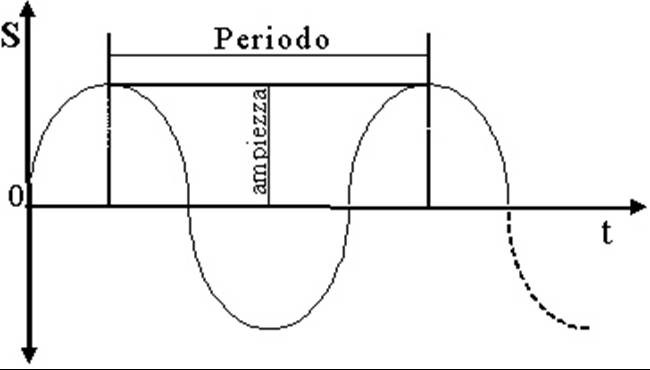
• la frequenza f dell’onda, cioè il numero di volte in cui avviene l’oscillazione di una molecola, nell’unità di tempo;

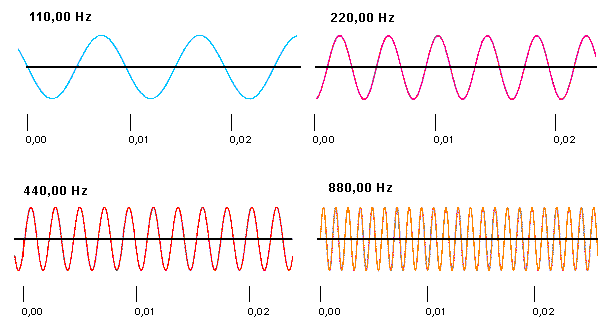
• la lunghezza d’onda λ (lambda) è la distanza che intercorre, in un certo istante, tra due zone consecutive di maggior addensamento, zone nelle quali la pressione acustica è massima;
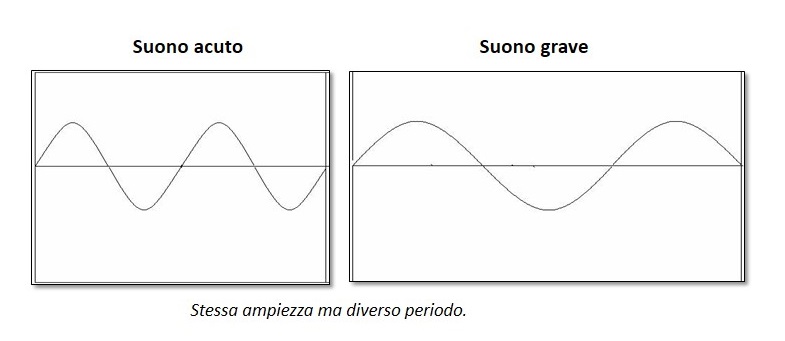
• l’ampiezza α (alfa) dell’oscillazione, cioè lo spostamento massimo delle molecole rispetto alla loro condizione di riposo, da cui deriva l’altezza (o acutezza) di un suono, dovuta alla rapidità delle vibrazioni che lo producono e consente di distinguere i suoni acuti da quelli gravi. Essa cambia a seconda della frequenza a cui l’onda vibra. Al crescere della frequenza corrisponde l’aumento dell’altezza. Onde sonore aventi uguali ampiezza ma frequenza diversa generano suoni di diversa altezza;

• la velocità v con cui la perturbazione avanza nel mezzo, come rapporto tra lambda e T.

Il sistema solare

Il nostro sistema solare, secondo le attuali conoscenze, è un sistema stellare di tipo planetario, costituito da un solo corpo celeste a luce propria, il Sole, otto satelliti principali, i pianeti, ciascuno con i relativi satelliti o meno, e due fasce di asteroidi: una interna tra Marte e Giove e l’altra esterna all’orbita di Nettuno, in cui si trovano anche diversi pianeti nani, quali Plutone e Sedna. La visione della sua organizzazione e strutturazione ha subito notevoli modifiche nel corso dei tempi, in quanto le conoscenze in possesso degli studiosi si sono via via ampliate e precisate a seguito delle osservazioni e delle implicazioni matematiche. Un primo modello geocentrico, o tolemaico, che poneva la Terra al centro dell’Universo conosciuto e tutti gli altri corpi celesti ruotanti intorno ad essa, ha dominato in molte civiltà antiche, come quella greca, fino al 1500, quando Niccolò Copernico (1473-1543) propose un modello di tipo eliocentrico, confermato quasi un secolo più tardi dalle scoperte fatte da Galileo Galilei (1564-1642) con il primo cannocchiale. Tra la fine del ‘500 e gli inizi del ‘600 Giovanni Keplero, fautore del sistema copernicano, ispirandosi alla geometria solida pitagorica, ricavò tre leggi, che ancora oggi descrivono il modello del moto dei pianeti del sistema solare:

1. L’orbita descritta da ogni pianeta nel proprio moto di rivoluzione è un’ellisse, di cui il Sole occupa uno dei due fuochi.
2. Durante il movimento del pianeta, il raggio che unisce il centro del pianeta al centro del Sole (raggio vettore) descrive aree uguali in tempi uguali.
3. Il quadrato del periodo di rivoluzione di un pianeta è proporzionale al cubo della sua distanza media dal Sole.

Questa terza legge, mettendo in relazione reciproca la velocità di un corpo celeste con la sua orbita, stabilisce anche un rapporto tra la velocità di corpi che si muovono su orbite differenti.

Il modello kepleriano trovò la sua definitiva giustificazione quando Isaac Newton nel 1687 pubblicò la sua legge sulla gravitazione universale, che dava una definitiva precisazione dell’equilibrio dinamico dell’intero sistema solare.

Breve glossario della musica

Nota: segno grafico che rappresenta simbolicamente un dato suono; In rapporto all’intonazione, le note sono indicate, in Italia e nei paesi latini, con le sillabe do, re, mi, fa, sol, la, si; mentre, in Germania e nei paesi anglosassoni, vengono anche indicate con le lettere dell’alfabeto, cominciando dal la (A) per finire con il sol (G).
Intervallo: differenza di altezza tra due suoni.
Accordo: esecuzione simultanea di due o più suoni di altezza diversa.
Consonanza: sensazione gradevole prodotta da due o più suoni eseguiti simultaneamente.
Dissonanza: sensazione sgradevole prodotta da due o più suoni eseguiti simultaneamente.

Matematica e musica

Il lavoro di ricerca di Keplero affonda le sue radici nella teoria della musica delle sfere, antico concetto filosofico che considerava l’universo come un immenso sistema di proporzioni numeriche, in cui i movimenti dei corpi celesti producevano una musica costituita da concetti armonico-matematici, non udibile dall’orecchio umano ma intellegibile dalla mente. La parola Musica trae origine dalle arti delle Muse, divinità della mitologia greca che vivevano sul monte Parnaso; essa è entrata profondamente nella scienza moderna, perché era già un elemento centrale della filosofia antica, come le concezioni greche di numero e di cosmo: era lo strumento che, attraverso l’udito, permetteva di intuire l’esistenza di un ordine universale e di comprendere le leggi della natura. Nel Medioevo, il filosofo e musicografo Severino Boezio, convinto che la Musica esprimesse l’ordine e l’armonia della totalità dei fenomeni naturali, a partire dal moto regolare dei cieli, espressione più alta di tale ordine, divise questa in tre grandi generi: musica del cosmo (mondana), dell’uomo (humana) e degli strumenti (instrumentalis), tre diverse realtà, interconnesse dal “potere dell’armonia”. Il Rinascimento è l’erede della tradizione pitagorico-platonica trasmessa da Boezio e, fino al cambiamento nei campi del sapere, la musica resta una scienza matematica che permette a filosofi, teologi, teorici musicali e scienziati di indagare l’universo e l’uomo. Nel Seicento, dopo la rivoluzione scientifica, la musica esce dal campo delle scienze per entrare definitivamente in quello delle arti e, con la nascita dell’estetica (1750), tale mutamento è accuratamente codificato.

Comunque sia, negli inconsapevoli ascoltatori di sempre il piacere e i sentimenti, che si provano nell’ascoltare un’ottava, sono matematicamente regolati.

Da Pitagora a Keplero

Il filosofo Pitagora del VI secolo a.C., considerato il padre della geometria e della matematica, fu il primo ad indagare le relazioni esistenti tra gli intervalli musicali e a parlare di Armonia. Una leggenda racconta che un giorno, passando davanti all’officina di un fabbro, notò che i martelli dell’artigiano, battendo il ferro sull’incudine, producevano echi in accordo tra loro e si accorse che le consonanze sonore erano in corrispondenza con rapporti numerici semplici. Tornato a casa, fissò un palo in una stanza diagonalmente da angolo ad angolo e vi appese quattro corde di uguale materiale, lunghezza e spessore, tese da pesi che avevano tra loro i rapporti dei martelli uditi in officina (i pesi erano di unità 6, 8, 9 e 12).  Battendo i pesi, rilevò che la differenza nell’altezza¹ dei suoni dipendeva dalla massa dei martelli e dal rapporto intercorrente tra le masse:

1 a 2 per i martelli che davano l’ottava
2 a 3 per quelli che davano la quinta
3 a 4 per quelli che davano la quarta
8 a 9 per il tono.

Questa constatazione lo portò a studiare la realizzazione di uno strumento che potesse renderne godibile l’effetto e tale studio si concluse con la costruzione del ‘‘monocorde’’, strumento costituito da una sola corda tirata su una struttura in legno, da cui ricavò che:

• una corda in vibrazione produce un suono la cui altezza è in stretta relazione con la lunghezza della corda stessa;
• una corda lunga produce una nota “bassa” o “grave”, al contrario una corda corta produce una nota “alta” o “acuta”;
•  ogni nota è contraddistinta da un numero proporzionale alla propria frequenza²

Da tali considerazioni Pitagora concluse che la divisione musicale creata dall’uomo dava origine all’espressione di rapporti ben determinati. Ad esempio, una corda divisa in 2 parti uguali, produce una nota di un’ottava³ più alta di quella prodotta dalla corda intera: le due parti uguali vibrano in un rapporto di 2 a 1 (2:1). Una corda divisa in 3 parti uguali vibra in un rapporto di 3 a 1 (3:1); se divisa in 4 parti uguali, crea un rapporto di 4 a 1 (4:1). Questo sistema di numerazione dei suoni, indicava che diverse “coppie” di note potevano essere tradotte in coppie di numeri e che le note che “stanno bene insieme” erano legate tra loro da un rapporto numerico semplice. 

Diatéssaron = intervallo di quarta (es. Do-Fa) 4/3 = 1.333
Diapénte = intervallo di quinta (es. Do-Sol) 3/2 = 1.5
Diàpason = intervallo di ottava (es. Do-Do) 2/1 = 2
Alcuni degli intervalli classificati da Pitagora.

Pitagora credeva che l’universo fosse un immenso monocorde con una sola corda tirata tra il cielo e la Terra, in cui l’estremità superiore era legata allo spirito assoluto, mentre quella inferiore era legata alla materia assoluta. Applicò così le sue leggi sugli intervalli armonici a tutti i fenomeni naturali, per dimostrare la relazione armonica insita in essi e, in particolare, in pianeti e costellazioni, introducendo il concetto di “musica delle sfere”. L’universo divenne così κόσμος, cioè “ordine”, poiché era possibile misurare ogni suo aspetto tramite il numero: questo era considerato un insieme di unità e l’unità equivalente al punto geometrico. Ne risultava che numeri e figure geometriche erano la stessa cosa: il tetraktys, la figura geometrica considerata sacra dai Pitagorici, esprimeva la perfezione di tale relazione nel numero 10.

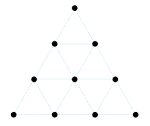
La musica era considerata la scienza dei rapporti. Dati quattro numeri a, b, c, d, si ha:
una proporzione aritmetica quando la somma dei medi è uguale a quella degli estremi, b + c = a + d;
una proporzione geometrica quando il prodotto dei medi è uguale a quello degli estremi, ac = bd;
una proporzione armonica quando i loro reciproci sono in proporzione aritmetica, 1/b + 1/c = 1/a + 1/d.

E questo ideale di proporzione e di simmetria, che regolava ogni aspetto del mondo, non era altro che il concetto di “armonia”.

Keplero

Il modello pitagorico rimase a lungo un punto di riferimento per la cosmologia, tanto che anche Keplero si rifece all’idea pitagorica e platonica dell’universo, quando intraprese la sua opera per confermare se lo schema dell’universo e delle sue parti potesse essere espresso in rapporti numerici e geometrici. Keplero ipotizzava che l’Universo fosse sede di fenomeni regolari, governati da leggi perfette e immutabili e comprensibili attraverso l’uso della ragione e della logica, e che il mondo e la natura fossero pervasi da ordine e armonia: una musica costituita da concetti armonico-matematici, non udibile dall‘orecchio umano ma intellegibile dalla mente. La sua ricerca della spiegazione dei moti dei pianeti del sistema solare partì dal modello eliocentrico del sistema copernicano, con l’analisi di alcune incongruenze presenti, quali la permanenza degli epicicli, che non offrivano una risposta corretta all’anomalo percorso dei pianeti intorno al Sole. Per vent’anni provò a dare un significato ai suoi dati e a quelli ricavati dalle osservazioni del suo maestro Tycho Brahe, per dimostrare che le orbite dei pianeti non potevano essere casuali, ma dovevano rispondere a precisi rapporti numerici, gli stessi che governano le leggi dell’armonia musicale e che consentono di distinguere un accordo piacevole all’udito da uno dissonante. Il lungo percorso lo portò a formulare le sue tre leggi sui movimenti dei pianeti, enunciate nelle tavole rudolfine (in onore dell’imperatore del Sacro Romano Impero Rodolfo II d’Asburgo) e pubblicate, le prime due su Astronomia Nova, un classico libro di astronomia, e la terza su Harmonices mundi,un testo che si occupava anche di musica e di astrologia.

Keplero cercò di rispondere alle numerose domande che si poneva, in merito alla determinazione del numero dei pianeti e alla grandezza delle loro distanze, attraverso la geometria che, dal punto di vista ontologico, considerava superiore all’aritmetica. E attraverso essa ricercò anche le corrispondenze tra l’armonica perfezione dei pianeti nel Sistema solare e le proporzioni espresse dalle consonanze musicali.

Dopo aver espresso queste ultime lungo una corda lineare, tipica del modello pitagorico, estese questo modello ad una corda chiusa, espressione delle orbite dei pianeti presenti nel sistema copernicano.

Ipotizzando la corda di uno strumento musicale richiusa in cerchio, determinò le consonanze attraverso gli archi descritti dai poligoni regolari inscrivibili e ricavabili con il compasso: i rapporti tra l’arco sotteso da uno dei lati e l’arco restante risultavano essere esattamente corrispondenti alle prime consonanze armoniche di ottava, quinta, quarta e terza maggiore. Moltiplicando i lati dei poligoni, ottenne anche i sotto-intervalli.

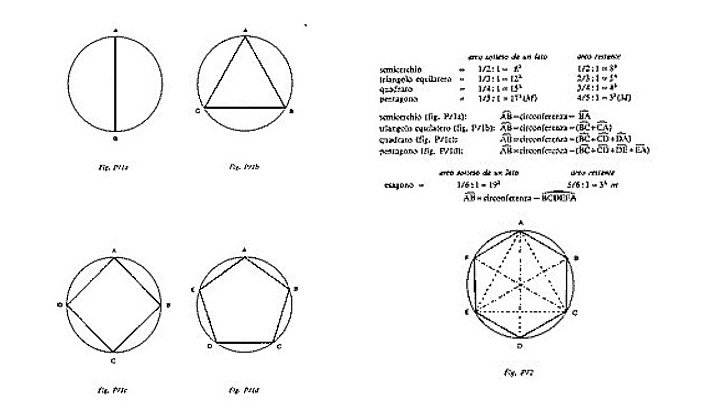
Ebbe l’intuizione che lo portò a questo modello durante la costruzione di un disegno che rappresentasse lo studio astrologico del fenomeno della grande congiunzione4 tra Giove e Saturno, nel triangolo formato dalle costellazioni Ariete, Leone e Sagittario⁵. Questi pianeti sono i più lenti e le loro congiunzioni le più rare: Giove si muove di 30° in un anno e Saturno di 12°, pertanto il primo guadagna 18° ogni anno sul secondo e lo raggiunge ogni venti anni. Seguendo tre principali grandi congiunzioni tra i due pianeti, si può evidenziare che, dato che Saturno compie in venti anni i 2/3 del suo percorso lungo lo zodiaco e Giove un giro completo e i 2/3 di un altro, esse si vengono a trovare a 243° di distanza tra loro lungo la circonferenza zodiacale, individuando tre punti, vertici di un triangolo equilatero. Keplero, dopo aver calcolato tutte le possibili grandi congiunzioni, sulla base di queste ricavò una figura, in cui notò che la costruzione di triangoli, non perfettamente equilateri, dava origine all’interno del disegno ad una seconda circonferenza concentrica.

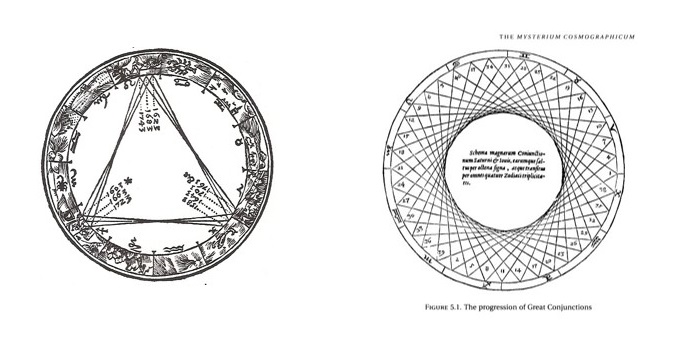
Notò, inoltre, che il rapporto tra i raggi dei due cerchi si avvicinava molto a quello esistente tra le distanze di Giove e Saturno dal centro dell’universo. Questo dato lo spinse a continuare la ricerca di altre analogie in questo senso, ipotizzando che vi potesse essere una correlazione tra i poligoni regolari inscritti in una circonferenza e le distanze dei pianeti dal Sole. Individuò, così, il pentagono tra Terra e Marte e l’esagono tra Terra e Venere; ma si accorse anche che le combinazioni possibili erano innumerevoli, mentre i pianeti intorno al Sole erano solo sei e, quindi, i rapporti solo cinque: Giove-Saturno, Marte-Giove, Terra- Marte, Venere-Terra, Mercurio-Venere.

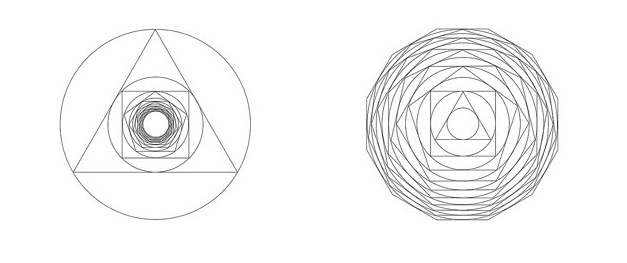
Inoltre, la presenza di figure piane tra quelle solide, rappresentate dalle sfere in cui erano considerati incastonati i pianeti, non costituiva un modello pienamente convincente.

Tuttavia non abbandonò l’idea di utilizzare figure geometriche nel suo studio ma la corresse, spostando l’attenzione sulle figure solide regolari, perché queste, come aveva dimostrato Euclide⁶  potevano essere solo cinque. Pubblicò questa intuizione nella sua opera giovanile, il Mysterium cosmographicum, stampata nel 1596 a Tubinga, dove parla dei cinque poliedri regolari, i cosiddetti “solidi platonici”: il tetraedro, il cubo, l’ottaedro, il dodecaedro e l’icosaedro, che sono gli unici poliedri inscrivibili in una sfera.

“La Terra è la sfera che misura ogni cosa.
Si costruisca un dodecaedro attorno ad esso: la sfera attorno ad esso sarà Marte.
Attorno a Marte si costruisca un tetraedro: la sfera attorno ad essa sarà Giove.
Attorno a Giove si costruisca un cubo: la sfera attorno ad esso sarà Saturno.
Ora si costruisca un icosaedro all’interno della Terra: la sfera inscritta sarà Venere.
All’interno di Venere si inscriva un ottaedro: la sfera al suo interno sarà Mercurio.”

Al centro di questo modello eliocentrico di universo chiuso e armonico, Keplero collocò il Sole e intorno ad esso circoscrisse le cinque sfere, su cui erano inseriti i cinque pianeti conosciuti. La Terra fu posta come discrimine tra i solidi stabili⁷ (cubo, tetraedro, dodecaedro), esterni alla sua orbita, e quelli più instabili (ottaedro, icosaedro), interni a essa. Le figure che costruivano l’angolo solido del primo gruppo di solidi (primari) erano diverse, mentre quelle che formavano l’angolo solido del secondo gruppo (secondari) erano triangoli e anche le facce dei solidi erano tutti triangoli. In questa riorganizzazione tutte le facce di ogni poliedro risultavano essere equidistanti dal centro e tangenti a una singola sfera inscritta e tutti gli angoli erano equidistanti dal centro e definivano una sfera circoscritta alle figure. Il rapporto tra i raggi delle due sfere, che erano riferite a ciascun poliedro, era ben definito e caratteristico: il tetraedro corrispondeva al rapporto più grande, perfettamente a 1:3; il cubo e l’ottaedro corrispondevano a 1:√3; il dodecaedro e l’icosaedro a 4:5. Sulla base di queste valutazioni ipotizzava, inoltre, che, se la sfera più esterna, quella di Saturno, aveva il raggio uguale all’orbita del pianeta, anche tutte le altre sfere avevano il raggio corrispondente all’orbita del proprio pianeta.

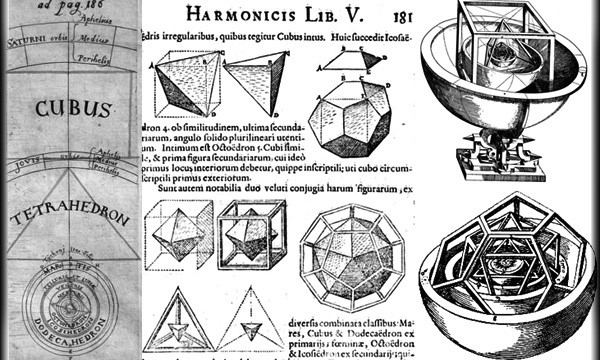
Questa ipotesi dava una giustificazione sia al numero delle orbite dei pianeti che alla loro distanza dal centro del sistema planetario, cioè il Sole, cui Keplero aveva attribuito la precipua capacità di regolare la diversa velocità dei pianeti a seconda della vicinanza o lontananza delle loro orbite da esso. Questa intuizione, però, doveva essere confermata anche dalle osservazioni per essere considerata valida.

“Quel che abbiamo detto fin qui serviva unicamente a sostenere la nostra tesi tramite argomenti di probabilità. Procederemo ora alla determinazione astronomica delle orbite e alle considerazioni geometriche. Se queste non confermano la tesi, i nostri sforzi precedenti saranno stati indubbiamente vani”.

Ma i calcoli dimostrarono tutt’altro: la posizione dei solidi regolari tra le orbite non concordava con le distanze ricavate dalle osservazioni fatte da Tycho Brahe, perché queste suggerivano distanze non perfettamente centriche di ogni pianeta nei confronti del Sole: le distanze reali differivano con errori perfino del 40%. Studiando l’orbita di Marte, Keplero riuscì a dimostrare che l’orbita del pianeta intersecava il Sole ad angolo fisso rispetto all’orbita della Terra e la velocità di spostamento intorno al Sole non era costante. In conseguenza a questi dati prospettò per Marte, dapprima, un’orbita ovale, poi una forma intermedia tra un uovo e un cerchio e, alla fine come una ellisse perfetta:

“a quel punto riuscii ad esprimere la cosa in forma di legge, semplice, elegante e vera:
le orbite planetarie sono delle ellissi e il Sole occupa uno dei fuochi.”

Abbandonò, così, definitivamente il modello faticosamente costruito, ma non rinunciò alla geometria. Si concentrò, infatti, sulla definizione delle orbite di forma ellittica percorse dai pianeti e, cercando di dimostrare che le cause delle eccentricità e dei periodi delle orbite dei pianeti corrispondevano a proporzioni armoniche (o consonanze), arrivò alla formulazione delle sue Tre Leggi. Le prime due furono pubblicate su Astronomia Nova nel 1609.

Prima legge: i pianeti descrivono orbite ellittiche, quasi complanari, aventi tutte un fuoco comune in cui si trova il Sole.
Seconda legge: il raggio che unisce il centro del Sole al centro di un pianeta (raggio vettore) descrive superfici uguali in intervalli di tempo uguali.

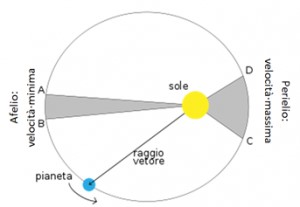
Keplero continuò a ricercare le proporzioni armoniche, prendendo in considerazione i seguenti elementi:

«1. La distanza dal sole; 2. I tempi periodici; 3. Gli archi di eccentrica giornalieri; 4. I ritardi in questi archi giornalieri; 5. Gli angoli col sole, ossia gli archi giornalieri apparenti, come sarebbero se visti dal sole».

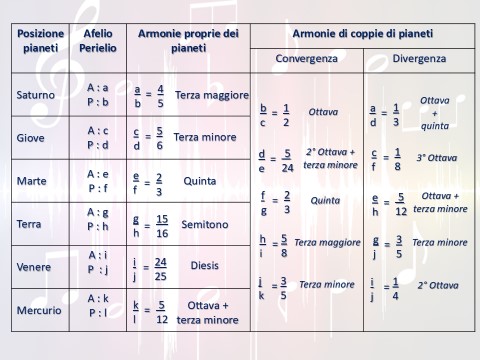
Riguardo al secondo elemento non riuscì ad evidenziare alcuna proporzione armonica; mentre nella valutazione del primo riscontrò intervalli concordanti con quelli musicali solo per Marte e Mercurio. Analizzando gli altri tre elementi, Keplero rilevò che la velocità dei pianeti variava in modo continuo da un massimo a un minimo ed ipotizzò che ad ogni velocità corrispondesse una frequenza e l’insieme di tutte le frequenze generasse una melodia. Ciascun pianeta, quindi, esprimeva una melodia propria, diversa per estensione in base all’eccentricità dell’orbita: la melodia di Mercurio, con l’orbita più ellittica, doveva risultare molto variegata; mentre quella di Venere, con orbita quasi circolare, monotona. Calcolò, allora, le ampiezze degli archi orbitali giornalieri percorsi da ciascun pianeta nei momenti più statici, cioè quelli di afelio e perielio, e confrontò i rapporti trovati tra loro con quelli degli intervalli musicali: erano corrispondenti. Per Saturno questo rapporto risultava circa 5:4, equivalente a una terza maggiore (do – mi), per Marte 3:2, quinta perfetta (do – sol), per la Terra 16:15, semitono diatonico (mi – fa).

Questa osservazione lo spinse a spostare la sua attenzione sulle ampiezze degli archi di orbita percorsi da due pianeti adiacenti, per valutare se producevano intervalli musicali. Utilizzando i valori rilevati nei momenti più statici, cioè quelli all’afelio e al perielio, calcolò i moti estremi convergenti, cioè quelli che sono negli apsidi più vicini di tutti e due (perielio del pianeta superiore e afelio dell’inferiore); e quelli divergenti, cioè quelli che sono agli apsidi opposti (afelio del pianeta superiore e perielio dell’inferiore).

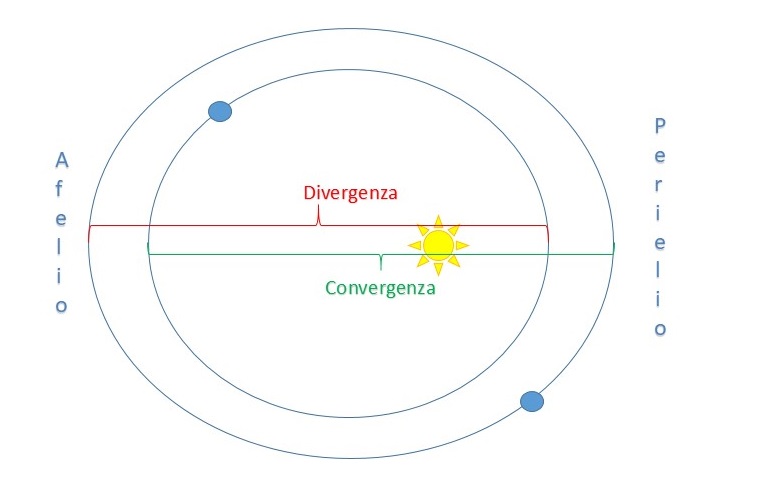
Ogni coppia di pianeti adiacenti, nel percorso della loro orbita, generano una melodia diversa nella loro divergenza (afelio per il più lontano dal Sole e perielio per il più vicino) e nella loro convergenza (perielio per il più distante e afelio per il più vicino).

Da questo ricavò la relazione che legava gli assi dell’ellisse e i periodi orbitali e arrivò alla formulazione della cosiddetta “legge armonica”, pubblicata nel 1619 in Harmonices mundi, libro 5 capitolo 3:

 “Res est certissima et exactissima, quod proportio quae est inter binorum quorumcumque Planetarum tempora periodica, sit praecise sesquialtera proportionis mediarum distantiarum”.
(È cosa certissima che la proporzione che lega i tempi periodici di ciascuna coppia di pianeti sia precisamente la proporzione sesquialtera delle distanze medie).

La proporzione sesquialtera consiste nel rapporto 3:2, il quale equivale esattamente all’intervallo di quinta perfetta che regge l’intero sistema musicale pitagorico.

Terza legge: i quadrati dei tempi che i pianeti impiegano a percorrere le loro orbite sono proporzionali ai cubi delle loro distanze medie dal Sole.

T ∝ r^3/2   

T² = kr³              T²/ r³ = k

T = tempo di rivoluzione
∝ = direttamente proporzionale
r = distanza media dal Sole
k = costante di proporzionalità

Keplero era pronto per scrivere il suo pentagramma.

Note

(1) Caratteristica percepita dall’orecchio umano che determina l’elevazione di un suono conseguente alla rapidità delle vibrazioni che lo producono.
(2) Grandezza che esprime il numero di eventi periodici al secondo.
(3) Intervallo relativo alla distanza fra due suoni uguali, di cui però uno è più grave e l’altro più acuto, cioè prodotto da vibrazioni di frequenza doppia.
(4) Posizione molto ravvicinata prospetticamente tra due pianeti, ne esistono diversi tipi.
(5) Uno dei trigoni, raggruppamenti importanti da un punto di vista astrologico, ricavati dalla divisione dello zodiaco in quattro gruppi di tre segni zodiacali o in quattro triangoli equilateri (Tolomeo, Tetrabiblos I,18).
(6) Euclide negli Elementi spiega che soltanto il triangolo equilatero, il quadrato e il pentagono regolare possono essere facce di poliedri regolari:

• In ciascun vertice devono convergere almeno tre facce (non esistono, infatti, angoloidi formati da uno o due poligoni).
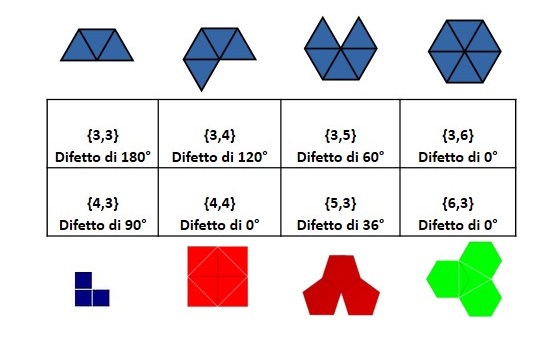
• In ogni angoloide la somma degli angoli delle facce deve essere minore di un angolo giro; la quantità che manca per formare i 360° è definita difetto.
• Trattandosi di poligoni regolari, ciascun vertice di ciascuna faccia può contribuire all’angoloide con massimo 360°÷3=120°.
• Ad avere angoli maggiori di 120° sono i poligoni con sei o più lati, pertanto possono formare solidi platonici solo il triangolo, il quadrato ed il pentagono. Ciascuna di queste figure si comporta differentemente:
  • a. Facce triangolari: gli angoli di un triangolo equilatero sono ampi 60°, quindi in un vertice del solido possono insistere 3, 4, o 5 triangoli; si formano, rispettivamente, il tetraedro, l’ottaedro e l’icosaedro.
    b. Facce quadrate: gli angoli di un quadrato sono ampi 90°, è quindi possibile far incontrare in un vertice 3 facce (3 x 90 = 270) ottenendo un cubo.
    c. Facce pentagonali: ogni angolo di un pentagono regolare misura 108°. È quindi possibile far incontrare in un vertice 3 facce (3 x 108 = 324) ottenendo un dodecaedro regolare.

(7) Nelle figure stabili l’asse di simmetria di rotazione intorno ad un asse passa per il centro di una faccia; mentre in quelle instabili passa per un angolo; per il tetraedro valgono entrambi i tipi di simmetria.

Bibliografia 

• Mario Livio, The Golden Ratio, Rizzoli 2003
• Bruce Stephenson, The Music of the Heavens – Kepler’s Harmonic Astronomy, Princeston Univeristy Press/ New Jersey, 1994.
• Gabriele Uggias, Keplero e la Musica. Il libro III dell’Harmonice Mundi (Linz, 1619): traduzione e introduzione, Alma Mater Studiorum/Università di Bologna, 2015.
• Alessandra Andreotti, Harmonia Mundi da Pitagora a Keplero – Musica e Astronomia, Accademia Lendinara, 2012.